Version
0.02 Last
updated 2002-07-03-15:18 -0700 (pdt)
The latest version of this document is always at http://Miser-theory.info/sketch/osketch.htm.
For a history of this document and its revisions, see Miser Note N020600:
Miser Sketch Notes.
Here is a brief sketch of the foundation for any
(and every) Miser system. This is the oMiser level because it
covers the elementary, ob structure only. It is devoted
exclusively to Obs, seemingly alone in a world unto themselves. This simple, closed structure is at the foundation of all
extensions that are introduced to achieve "higher" levels.
oMiser and ob
provide a rich yet spare environment. oMiser is the launchpad for distinguishing how much we rely on the familiar and how much is overlooked in our everyday approach to computation, theories, logic,
mathematics and especially to language itself.
Content
We want to put something up top about what we are doing here, and the
viewpoint that we want to encourage.
Two ways we want to look at Obs and the basic provisions of the
Miser system.
We have a computer implementation in mind. But it is
abstracted. Still a computer implementation, but not a fixed
implementation. So I will illustrate the computational nature of Miser by
informal means: diagrams, descriptions of behavior of a computer, and so on.
At the same time, there is also a theoretical system, a
mathematical structure, that the computational system honors in a particular
way.
I will give informal characterizations of the computational
system, using diagrams that are to be suggestive of valid interpretations
of the theory.
I will also give informal expression to the theoretical system
of which the computational system is to be a valid interpretation.
This illustrates how these two views can be brought together in
demonstration of what it means to manifest abstractions (theoretical entities) by
computational means. This sets the stage for a rigorously developed
manifestation in operational computer software and for a formally developed
exploration of the theoretical system that is its foundation.
It is important to notice that the theory is being developed with an
implementation in mind. I am interested in the operational capabilities of
the kind of system that I envision, while at the same time the development of a
theoretical system sharpens understanding and also provides a venue for
exploring the way that theory and reality can be said to collide in the
computer. The egg and the chicken have no existence apart.
We mean by this that Obs are
sufficient. In principle, we don't need anything more to provide a
universal system of computation. It is neither practical nor desirable to
limit ourselves this way. We start here because this is the place where we
can reveal exactly what is involved in manifesting anything via computation and
then what is or is not remarkable by extensions that deliver computation on
more-familiar terms that, nevertheless, preserve Obs and their power.
|
Here it is argued that comparison, knowledge of existence, and understanding
of number, are essential to knowledge, but cannot be included in perception
since they are not affected through any sense organ.
|
-- Bertrand Russell on Knowledge and Perception in Plato.
1.1 Identity and Existence
This section provides a basic flavor of the approach and how we
will toggle between several perspectives, always endeavoring to keep them
distinct.
1.1.1 Theoretical Structure
The
structure, ob = Ob, Of, Ot consists of
-
a set, Ob, of elements (the individual Obs),
-
a set, Of, of functions over Ob
-
and a formal system, Ot, with initial axioms
that provides everything and only what there is to be (formally) known about
ob.
1.1.2 Informal Conception
There are Obs. That's all we get to know for
now. Don't assume anything. And don't confuse the notion of Obs with
anything that you might already know about objects or "objects" or
object-oriented programming or anything else. We'll look for prospective
connections later. For now, consider that, with oMiser, Obs have no
relationship to classes and objects the way they are spoken of by software
developers.
 For
now, there is very little to know about Obs. They are some kind of
(abstract) thing. We will indicate how little we know by depicting an
arbitrary Ob as a cloud-like entity.
For
now, there is very little to know about Obs. They are some kind of
(abstract) thing. We will indicate how little we know by depicting an
arbitrary Ob as a cloud-like entity.
It is fundamental that there appear be many Obs -- an unlimited
number, actually -- and
however they come to our attention, they are distinguished in some way. When the same Ob comes to our attention in more than one way,
it is always recognizable as the same Ob. That's an essential quality for all interpretations that we
want to allow.
our attention, they are distinguished in some way. When the same Ob comes to our attention in more than one way,
it is always recognizable as the same Ob. That's an essential quality for all interpretations that we
want to allow.
This conception is reflected in the theory by the rules for identity
and distinction. It is not a complete formulation and we will ultimately
give this topic much closer scrutiny.
One thing to pick
up on later is that it is the structure that is the "whole" and when
we have our attention on individuals, speaking conceptually or in the language
of the theory, that should be taken as a way of viewing aspects of the
whole. Although we speak of individuation, and speak of Ob as a set, it is
not that Obs (that is, the members of the conceptual set, Ob) have an
independent existence. Quote [Quine].
Also, ensure that
we do not speak in a way that implies some sort of Platonic existence of
Obs. We will be neutral on that matter, and will speak in a way where
Platonic existence is absolutely unnecessary in what we do here. Have it
be imagined Obs, if necessary.
1.1.3 The Axioms of Identity for Obs
There is an equivalence relationship defined over Obs.
There are no other entities in ob, so it is safe to use the common
symbol "=" for this relationship: Ob identity. 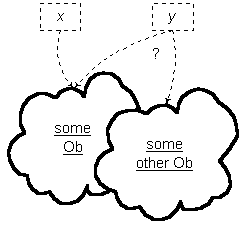 The
intended interpretation of x = y is that Ob x is Ob y.
The
intended interpretation of x = y is that Ob x is Ob y.
1.1.3.1 [Reflexivity] If x is an Ob, x = x.
1.1.3.2 [Symmetry] For any Obs x and y, if
x = y, then y = x.
1.1.3.3 [Transitivity] For any Obs x, y
and z, if x = y and y = z, then x = z
1.1.3.4 [Distinction] x ¬= y is
equivalent to ¬(x = y) by definition. The intended
interpretation of x ¬= y is that Ob x is not Ob y,
which is to say that Ob x and Ob y are distinct.
1.1.3.5 [Identity Completeness] For any Obs x
and y, it is the case that
(x
= y or x ¬= y) and ¬(x = y and x ¬= y).
The identity-completeness condition is introduced to establish
that whether or not the law of excluded middle holds for
propositions in general, it does apply for identity, and identity applies among all Obs. This places a strong condition on any valid
interpretation of ob, and is part of the assurance of a sound computational manifestation for Obs.
[Find a better term if sound is inappropriate or misleading here.]
1.1.4 Computational Manifestation of Obs
[Rework this part to have it that manifestations are erected
and discarded as part of computations, but it is as if ob is
always there. The manifestations preserve this illusion. Also,
make it simpler and not so heavy. Finally, point out that it is an
oMiser software library that provides the necessary manifestation.
Later, we will even consider that, among all computers on which some
manifestations of ob are realized, there is every indication that
it is the one and only ob structure. We get to look at the
Platonic illusion. This may belong in separate notes, but I want to
remind myself to keep my use of language consistent with that prospect.]
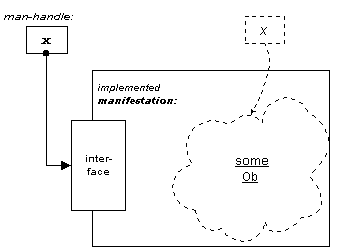 Obs
will be represented in the processes of conventional digital computers.
This is accomplished by organization of computer memory and software in such a
way that Obs are manifest in the operation of the digital computer.
The manifestations constitute a valid interpretation of ob.
Obs
will be represented in the processes of conventional digital computers.
This is accomplished by organization of computer memory and software in such a
way that Obs are manifest in the operation of the digital computer.
The manifestations constitute a valid interpretation of ob.
[Make sure we define this sense of interpretation somewhere up
near the beginning. It relates to the identity and existence
conversation.]
Manifestations are delivered through the oMiser software
library created for operation with conventional computer programs. The library
procedures deliver interfaces to manifestations of Obs. Through
operations at the interfaces, all behavior is as if the Obs are actually
present somewhere "behind" the interfaces of the manifestations. The manifestations
operate successfully as representatives of the Obs in the processing environment of the
conventional computer system.
Typically, a computer storage location serves as a placeholder
for a manifestation. The storage holds a man-handle of some kind.
The man-handle serves to locate a particular manifestation (interface).
Man-handle storage elements are the means to keeping track of the Ob
manifestations that a computer program is accessing.
In an operating computer system, different man-handle storage
might refer to the same manifestation interface. Different interfaces might
provide manifestation of the same Ob. The form of identity maintained for
computer storage, interfaces, and handles to interfaces is generally
independent of the identity and distinction among the manifest Obs -- there
are different worlds or domains involved.
Part of a particular manifestation methodology is provision of
an oracle that can confirm whether the manifestations accessible
through two manifestation interfaces or two man-handles are for manifestations
of the same Ob or
not. oMiser provides such an oracle. That is, the identity of the
manifest Obs is always determined. [Watch that language.]
The possession of a valid man-handle to a manifestation
interface establishes the existence of the particular manifest Ob. Obs
may have persistence beyond the existence of any manifestation and can reoccur
as the Obs of subsequent manifestations. When we have a man-handle, we
say that the Ob is determined. Much of what we say about the
computational model revolves around an Ob being determined. There are
operations that one can carry out with manifestations where an Ob cannot be
determined, and no result is delivered. That is to say, oMiser never
delivers a man-handle for a seeming manifestation that has no determined
Ob. It just doesn't happen. We will discuss later what happens
instead, if anything.
1.1.5 Existence
Talk in the computational and informal conceptions first.
There is nothing to say about this in the theory, at this
point. It is the interpretation/manifestation that gives existence to the
extent there is such a thing.
We will strengthen this requirement when we assert that the
definite, determined object ob-NULL
is in Ob.
Later, we get to look at how manifestation of ob-NULL
(or any other, but this one is assured) gives rise to all of ob,
that Obs live only in ob and are not reduced or separatable.
This is the case for ob-manifestation.
1.2 Basics - Informal Theory
The use of x ¶ y is an ordering on Obs.
The intended interpretation of x ¶ y is that Ob x is
prior to Ob y. An important consequence is that if x ¶ y,
then Ob x must be distinct from Ob y.
We don't know exactly where we will introduce that. We
will actually deliver functions a and b first, then go into other cases.
If z = c(x, y), then x ¶ z and y ¶ z.
If z = s(x), then x ¶ z.
If x ¶ y and y ¶ z, then x ¶ z
If x ¶ y, then ¬(y ¶ x)
If x = y, then ¬(x ¶ y)
a(z) = z or a(z) ¶ z
b(z) = z or b(z) ¶ z
c(x, y) = c(m, n) if-and-only-if x = m and y = n
s(x) = s(m) if-and-only-if x = m
1.1.1.2 The set of Obs is closed with respect to the
primitive Ob functions a, b, c, and s. The primitive functions are
well-defined and total.
1.1.1.7 The individuals, singletons, and combinations
partition the Obs. Every Ob is exactly one of these.
1.3 Combinations
1.3.1 If z = c(x, y), then a(z)
= x and b(z) = y and z is a combination.
1.3.2 For any Ob z, z = c(a(z), b(z)) if and only if
z is a
combination.
1.3.3 We define is-combination(z) to be
equivalent to z = c(a(z), b(z))
1.4 Singletons
If z = s(x), then a(z) = x and b(z)
= z
1.1.1.6 For any Ob z, If a(z) = z and b(z)
= z, then z is a singleton and z = s(a(z)).
1.5 Individuals
1.1.1.5 For any Ob z, If a(z) = z
and b(z) = z, then z is an individual.
1.6 Why All We Need
We have described all of the primitive functions of ob but
one. It is asserted that these functions, with =, provide a
complete theory for Obs, given some way to characterize all the effective
procedures that there are on Obs.
oApply: Ob x Ob -> Ob is in Of.
oEval: Ob x Ob x Ob -> is in Of.
[Include the oApply-oEval mutual recursion definition.]
The limitations of operating with Ob manifestations because there is no
externally/humanly-meaningful function. We can represent everything, but
communicate almost nothing. We don't even have the formalism of Ob
theory available. We just have raw access to the manifestation of Ob,
not the formalism (or metalanguage) in which we have been expressing Obs.
The idea of persistent description of Obs. That will be later. We
can "write" Obs in XML and we can "write" Obs in the
scripting language, Frugal.
More than that, there is the use of the Applicative Interpretation model,
and its extensions, to connect to the world in extremely useful, some might
say meaningful, ways.
Building-out and bridging will happen in this progression.
First, we will develop [o]Frugal, a scripting language that allows us to
express oMiser computations in something that is shareable among people and
that provides an external language that we can use to quickly manifest an Ob
and exercise it in breadboard/prototype mode.
We will also develop obXML, a format in XML for expressing an [o]Miser Ob
such that it can be exchanged and then (re-) manifest on the same or different
computers at later times. The idea of manifestation elsewhere and
re-manifestation will provide interesting considerations.
With oMiser, there is no identified way, internal to Ob,
to deal with symbols. So there is no way to deliver symbols to oMiser
and create computations that work with those symbols and incorporate symbols
in the result. This impairs our ability, using Ob itself, to
provide formal manipulations (still on Obs) and that allow us to have Obs be
convenient expressions for forms that are tied to the intended purpose of
having our computations be interpretations of other important theories:
arithmetic, logic, and applications that arise in the purposive use of
computation. The inputs and results are still Obs, but we have a form of
individuals that makes Obs useful as symbolic expressions that are tied
to the purpose of an oMiser computation. This takes us to the sMiser level.
This is done by establishing a family of individual obs that provide an
external-world identity, expressed as a spelled symbol.
sMiser is accompanied by [s]Frugal, a scripting language that allows us to
take advantage of symbols (for people) in commanding Miser computations and
operating in the enriched sMiser world. (An [o]Frugal version exists
merely as a prototype fixture for exercising oMiser and obtaining obXML as a
way to save and restore our early work.)
sMiser is a baby step toward the development of iMiser, an
interactive/imperative system. It deals with important considerations of
language, identity, and the use of symbols that are not normally separated
out. We have a world without symbols, then we extend oMiser with symbols
that allow an interesting external sense of identity. We have not
actually done anything, but the result is far more convenient.
We now discuss the fact that every individual has an applicative
interpretation. Now, in oMiser, the application of any Ob to an Ob,
produces an Ob. This would appear to not be very fruitful.
Consider that an individual Ob can be the Ob manifestation of
an object in some other system than Ob. We cannot see,
directly in the Ob manifestations, what these other
manifestations are. But whatever they accomplish, if we have a complete
primitive set of operations on them, also provided via Ob manifestations, we
know that we can create every computable function on those objects
using the already-established computational completeness of oMiser for
computations on Obs.
This is a giant leap, and better motivational examples will be
needed. It also helps to have Frugal-ese and sMiser to appeal to.
Which new kinds of theories do we manifest this way. Well, for
starters, the ones that let us express sFrugal and obXML processing in Ob
itself.
-
- [More1979]
- More, Trenchard. Various technical reports and conference papers.
Find his use of individuals and singletons and
construct a reference for it. It should be in the APL 79 proceedings
and in IBM research papers before that. Iverson may have incorporated
that into something by now, too. [I still have a file folder on Array
Theory. Look there.]
- [Proskurowski1980]
- Proskurowski, Andrzej. On the Generation of Binary Trees. J.
ACM 27, 1 (January 1980), 1-2. [Tear sheet in file on
sorting]
- [Quine???]
- Set Theory and Its Logic reference. Capture the quote about classes
and individuation not requiring separation
- [Rosenbloom1950]
- Rosenbloom, Paul C. The Elements of Mathematical Logic.
Dover (New York: 1950).
My expression of combinatory algebra is based on
that given in Rosenbloom's Chapter 3 section on combinatory logics.
- [Russell-PlatoQuote]
- Russell, Bertrand. On Knowledge and Perception in Plato. Now
where the heck did he say that.
- [Solomon1980]
- Solomon, Marvin., Finkel, Raphael A. A Note on Enumerating Binary
Trees. J. ACM 27, 1 (January 1980), 3-5. [Tear
sheet in file on sorting]
- [Strachey-McG]
- Strachey, Christopher. The McG Paper on macro generation, British
Computer Journal. Find that puppy again.
-
- version 0.02 2002-07-03 (orcmid)
- Complete the first round on identity and start filling in later
sections with placeholders and basic notes, but not developed beyond
giving some statements of my intentions. This version is broken
off after a crash leaves me having to recreate changes here. This
provokes my providing more-careful attention to preserving history and
archiving of versions even though this is still a crude progression
before the sketch is ready for daylight. I also want to make it
available for early review and discussion with associates.
- version 0.01 2002-06-21 (orcmid)
- Start building the basic sketch so that people who are familiar with this kind of
system can get a sense of it until I stitch more in here and build out the
notes that have already been identified/started. There will also be
additional notes to support the sketch.
created 2002-06-16-18:31 -0700 (pdt) by orcmid
$$Author: Orcmid $
$$Date: 02-07-03 18:22 $
$$Revision: 16 $
Home
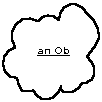 For
now, there is very little to know about Obs. They are some kind of
(abstract) thing. We will indicate how little we know by depicting an
arbitrary Ob as a cloud-like entity.
For
now, there is very little to know about Obs. They are some kind of
(abstract) thing. We will indicate how little we know by depicting an
arbitrary Ob as a cloud-like entity. our attention, they are distinguished in some way. When the same Ob comes to our attention in more than one way,
it is always recognizable as the same Ob. That's an essential quality for all interpretations that we
want to allow.
our attention, they are distinguished in some way. When the same Ob comes to our attention in more than one way,
it is always recognizable as the same Ob. That's an essential quality for all interpretations that we
want to allow. The
intended interpretation of x = y is that Ob x is Ob y.
The
intended interpretation of x = y is that Ob x is Ob y. Obs
will be represented in the processes of conventional digital computers.
This is accomplished by organization of computer memory and software in such a
way that Obs are manifest in the operation of the digital computer.
The manifestations constitute a valid interpretation of ob.
Obs
will be represented in the processes of conventional digital computers.
This is accomplished by organization of computer memory and software in such a
way that Obs are manifest in the operation of the digital computer.
The manifestations constitute a valid interpretation of ob.